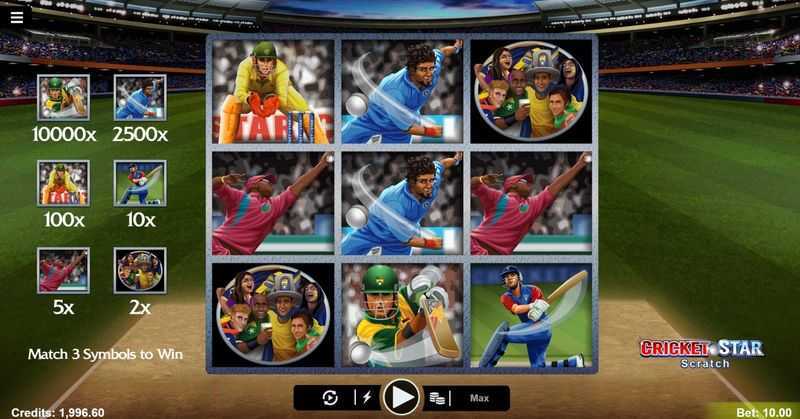
How to Play Cricket Star Slot for Real Money Online

Michael Carter

Published: May 1, 2025

1. RTP (Return to Player): 97%

The RTP of 97% indicates that for every 100 units wagered, a player can typically expect to recover 97 units over the long run. The remaining 3 units account for the house edge. This RTP value is considered quite favorable for players, suggesting a reasonable playability and potential for decent returns.

2. Grid Structure: 5-3

The 5-3 grid means that the slot features 5 reels with 3 rows each. This structure, combined with 243 paylines, employs a 'ways to win' system. Such configurations often lead to a high number of winning combinations on each spin, which can result in frequent, albeit potentially smaller, wins.

3. Max Bet Scenario:

Placing the maximum bet of 0.10 is possible in this slot. The total maximum win is not specified; however, it can be calculated based on the RTP and expected payouts. Assuming an average win of 97% return over numerous spins, if hypothetically all outcomes are favorable, the primary concern remains the volatility which suggests moderate risk.

If we consider a spin with the maximum bet:

- Bet: 0.10

- Expected Return: 0.10 * 0.97 = 0.097, or 9.7 cents per spin on average when accounting for the RTP.

Maximum win in practice could vary greatly depending on the game's top multipliers which are unspecified.

4. Minimum Bet: 0.01

With a minimum bet of 0.01, the potential returns per spin can also be calculated in a similar fashion. The expected return from the lowest bet would be:

- Bet: 0.01

- Expected Return: 0.01 * 0.97 = 0.0097, or 0.97 cents per spin on average.

Simple Expected Return Calculation:

Suppose a player spins 1,000 times with a 0.10 bet, their total wager would be 100 coins. Based on the RTP of 97%, we would estimate the expected return as follows:

Expected loss = 3 coins

This assessment means the player is likely to incur a 3 coins loss over 1,000 spins. However, outcomes can be cyclical, leading to moments of variance where substantial wins could be obtained.

Cricket Star Slot Machine – Screenshots