How to Play Midas Gold Slot for Real Money Online

Michael Carter

Published: April 26, 2025

1. RTP (Return to Player): 95.22%

The RTP of Midas Gold stands at 95.22%, meaning that, on average, players can expect to receive back approximately 95.22 coins for every 100 coins wagered. The remaining 4.78 coins represent the house edge. While this RTP is reasonable, it indicates that players may experience significant variance in returns over the short term due to the high volatility.

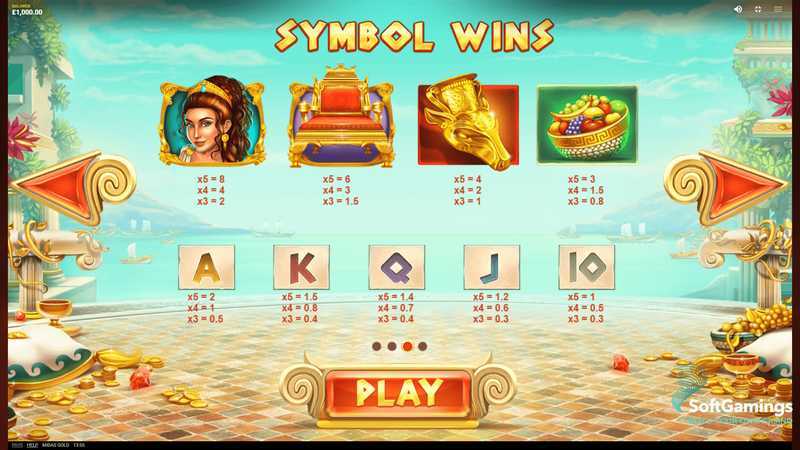
2. Paylines: 243

Midas Gold utilizes a 243 ways to win structure, which allows players to achieve winning combinations in multiple directions. This setup supports frequent wins compared with traditional fixed paylines, though the presence of high volatility may affect the size of those wins, leading to fewer and potentially larger payouts.

3. Maximum Bet Scenario:

Placing the maximum bet of $500 gives players a chance to win the highest possible payout, capped at $2,000. This cap indicates that the maximum win is limited despite the high bet, reflecting careful balancing by the provider in relation to the game's volatility. Hence:

Maximum win: $2,000 is representational and shows that while the bet amount is high, the win potential is capped, signaling caution in upscaling bets significantly.

4. Minimum Bet: $0.20

The minimum bet provides an entry point for players looking to manage risk. With a minimum stake of $0.20, the maximum theoretical payout remains at $2,000, translating to:

Notably, the payout multiplier for the max win still sits at $2,000 irrespective of the betting size, making it intriguing for players to weigh risks versus returns.

Simple Expected Return Calculation:

Assuming a player spins 1,000 times with a $1 bet (total wager: $1,000). With an RTP of 95.22%:

The expected loss in this situation would be:

Expected loss = $47.80

This reflects the player’s anticipated return in the short run. However, it's essential to note that slot performance can fluctuate significantly due to the inherent randomness of each spin.

Midas Gold Slot Machine – Screenshots